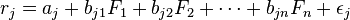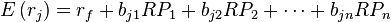Arbitrage pricing theory

Arbitrage pricing theory

In finance, arbitrage pricing theory (APT) is a general theory of asset pricing, that has become influential in the pricing of stocks.

APT holds that the expected return of a financial asset can be modeled as a linear function of various macro-economic factors or theoretical market indices, where sensitivity to changes in each factor is represented by a factor-specific beta coefficient. The model-derived rate of return will then be used to price the asset correctly – the asset price should equal the expected end of period price discounted at the rate implied by the model. If the price diverges, arbitrage should bring it back into line.

The APT model

Risky asset returns are said to follow a factor structure if they can be expressed as:



where

• a_j is a constant for asset j

• F_k is a systematic factor

• b_jk is the sensitivity of the jth asset to factor k, also called factor loading,

• and ε_j is the risky asset’s idiosyncratic random shock with mean zero.

Idiosyncratic shocks are assumed to be uncorrelated across assets and uncorrelated with the factors.

The APT states that if asset returns follow a factor structure then the following relation exists between expected returns and the factor sensitivities:



where

• RP_k is the risk premium of the factor,

• r_f is the risk-free rate,

That is, the expected return of an asset j is a linear function of the assets sensitivities to the n factors.

Note that there are some assumptions and requirements that have to be fulfilled for the latter to be correct: There must be perfect competition in the market, and the total number of factors may never surpass the total number of assets (in order to avoid the problem of matrix singularity),

Arbitrage mechanics

In the APT context, arbitrage consists of trading in two assets – with at least one being mispriced. The arbitrageur sells the asset which is relatively too expensive and uses the proceeds to buy one which is relatively too cheap.

Under the APT, an asset is mispriced if its current price diverges from the price predicted by the model. The asset price today should equal the sum of all future cash flows discounted at the APT rate, where the expected return of the asset is a linear function of various factors, and sensitivity to changes in each factor is represented by a factor-specific beta coefficient.

A correctly priced asset here may be in fact a synthetic asset – a portfolio consisting of other correctly priced assets. This portfolio has the same exposure to each of the macroeconomic factors as the mispriced asset. The arbitrageur creates the portfolio by identifying x correctly priced assets (one per factor plus one) and then weighting the assets such that portfolio beta per factor is the same as for the mispriced asset.

When the investor is long the asset and short the portfolio (or vice versa) he has created a position which has a positive expected return (the difference between asset return and portfolio return) and which has a net-zero exposure to any macroeconomic factor and is therefore risk free (other than for firm specific risk). The arbitrageur is thus in a position to make a risk-free profit:

Where today’s price is too low:

The implication is that at the end of the period the portfolio would have appreciated at the rate implied by the APT, whereas the mispriced asset would have appreciated at more than this rate. The arbitrageur could therefore:

Today:

1 short sell the portfolio

2 buy the mispriced asset with the proceeds.

At the end of the period:

1 sell the mispriced asset

2 use the proceeds to buy back the portfolio

3 pocket the difference.

Where today’s price is too high:

The implication is that at the end of the period the portfolio would have appreciated at the rate implied by the APT, whereas the mispriced asset would have appreciated at less than this rate. The arbitrageur could therefore:

Today:

1 short sell the mispriced asset

2 buy the portfolio with the proceeds.

At the end of the period:

1 sell the portfolio

2 use the proceeds to buy back the mispriced asset

3 pocket the difference.

Relationship with the capital asset pricing model (CAPM)

The APT along with the capital asset pricing model (CAPM) is one of two influential theories on asset pricing. The APT differs from the CAPM in that it is less restrictive in its assumptions. It allows for an explanatory (as opposed to statistical) model of asset returns. It assumes that each investor will hold a unique portfolio with its own particular array of betas, as opposed to the identical "market portfolio". In some ways, the CAPM can be considered a "special case" of the APT in that the securities market line represents a single-factor model of the asset price, where beta is exposed to changes in value of the market.

Additionally, the APT can be seen as a "supply-side" model, since its beta coefficients reflect the sensitivity of the underlying asset to economic factors. Thus, factor shocks would cause structural changes in assets’ expected returns, or in the case of stocks, in firms’ profitabilities.

On the other side, the capital asset pricing model is considered a "demand side" model. Its results, although similar to those of the APT, arise from a maximization problem of each investor’s utility function, and from the resulting market equilibrium (investors are considered to be the "consumers" of the assets).