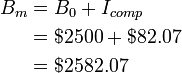Interest is a fee paid by a borrower of assets to the owner as a form of compensation for the use of the assets. It is most commonly the price paid for the use of borrowed money, or, money earned by deposited funds.
When money is borrowed, interest is typically paid to the lender as a percentage of the principal, the amount owed. The percentage of the principal that is paid as a fee over a certain period of time (typically one month or year), is called the interest rate. A bank deposit will gain interest because the bank is paying for the use of the deposited funds. Assets that are sometimes lent with interest include money, shares, consumer goods through hire purchase, major assets such as aircraft, and even entire factories in finance lease arrangements. The interest is calculated upon the value of the assets in the same manner as upon money.
Interest is compensation to the lender, for a) risk of principal loss, called credit risk; and b) forgoing other useful investments that could have been made with the loaned asset. These forgone investments are known as the opportunity cost. Instead of the lender using the assets directly, they are advanced to the borrower. The borrower then enjoys the benefit of using the assets ahead of the effort required to obtain them, while the lender enjoys the benefit of the fee paid by the borrower for the privilege. In economics, interest is considered the price of credit.
Interest is often compounded, which means that interest is earned on prior interest in addition to the principal. Compound interest grows at an exponential rate and its mathematical study led to the discovery of the number e.
Types of interest
Simple interest
Simple interest is calculated only on the principal amount, or on that portion of the principal amount that remains unpaid.
The amount of simple interest is calculated according to the following formula:
where r is the period interest rate (I/m), B0 the initial balance and m the number of time periods elapsed.
To calculate the period interest rate r, one divides the interest rate I by the number of periods m.
For example, imagine that a credit card holder has an outstanding balance of $2500 and that the simple interest rate is 12.99% per annum. The interest added at the end of 3 months would be,
and he would have to pay $2581.19 to pay off the balance at this point.
If instead he makes interest-only payments for each of those 3 months at the period rate r, the amount of interest paid would be,
His balance at the end of 3 months would still be $2500.
In this case, the time value of money is not factored in. The steady payments have an additional cost that needs to be considered when comparing loans. For example, given a $100 principal:
- Credit card debt where $1/day is charged: 1/100 = 1%/day = 7%/week = 365%/year.
- Corporate bond where the first $3 are due after six months, and the second $3 are due at the year’s end: (3+3)/100 = 6%/year.
- Certificate of deposit (GIC) where $6 is paid at the year’s end: 6/100 = 6%/year.
There are two complications involved when comparing different simple interest bearing offers.
- When rates are the same but the periods are different a direct comparison is inaccurate because of the time value of money. Paying $3 every six months costs more than $6 paid at year end so, the 6% bond cannot be ‘equated’ to the 6% GIC.
- When interest is due, but not paid, does it remain ‘interest payable’, like the bond’s $3 payment after six months or, will it be added to the balance due? In the latter case it is no longer simple interest, but compound interest.
A bank account that offers only simple interest, that money can freely be withdrawn from is unlikely, since withdrawing money and immediately depositing it again would be advantageous.
Compound interest
Compound interest is very similar to simple interest; however, with time, the difference becomes considerably larger. This difference is because unpaid interest is added to the balance due. Put another way, the borrower is charged interest on previous interest. Assuming that no part of the principal or subsequent interest has been paid, the debt is calculated by the following formulas:
where Icomp is the compound interest, B0 the initial balance, Bm the balance after m periods (where m is not necessarily an integer) and r the period rate.
For example, if the credit card holder above chose not to make any payments, the interest would accumulate
So, at the end of 3 months the credit card holder’s balance would be $2582.07 and he would now have to pay $82.07 to get it down to the initial balance. Simple interest is approximately the same as compound interest over short periods of time, so frequent payments are the least expensive repayment strategy.
A problem with compound interest is that the resulting obligation can be difficult to interpret. To simplify this problem, a common convention in economics is to disclose the interest rate as though the term were one year, with annual compounding, yielding the effective interest rate. However, interest rates in lending are often quoted as nominal interest rates (i.e., compounding interest uncorrected for the frequency of compounding).
Loans often include various non-interest charges and fees. One example are points on a mortgage loan in the United States. When such fees are present, lenders are regularly required to provide information on the ‘true’ cost of finance, often expressed as an annual percentage rate (APR). The APR attempts to express the total cost of a loan as an interest rate after including the additional fees and expenses, although details may vary by jurisdiction.
In economics, continuous compounding is often used due to its particular mathematical properties.
Fixed and floating rates
Commercial loans generally use simple interest, but they may not always have a single interest rate over the life of the loan. Loans for which the interest rate does not change are referred to as fixed rate loans. Loans may also have a changeable rate over the life of the loan based on some reference rate (such as LIBOR and EURIBOR), usually plus (or minus) a fixed margin. These are known as floating rate, variable rate or adjustable rate loans.
Combinations of fixed-rate and floating-rate loans are possible and frequently used. Loans may also have different interest rates applied over the life of the loan, where the changes to the interest rate are governed by specific criteria other than an underlying interest rate. An example would be a loan that uses specific periods of time to dictate specific changes in the rate, such as a rate of 5% in the first year, 6% in the second, and 7% in the third.
Composition of interest rates
In economics, interest is considered the price of credit, therefore, it is also subject to distortions due to inflation. The nominal interest rate, which refers to the price before adjustment to inflation, is the one visible to the consumer (i.e., the interest tagged in a loan contract, credit card statement, etc.). Nominal interest is composed of the real interest rate plus inflation, among other factors. A simple formula for the nominal interest is:
i = r + π
Where i is the nominal interest, r is the real interest and π is inflation.
This formula attempts to measure the value of the interest in units of stable purchasing power. However, if this statement were true, it would imply at least two misconceptions. First, that all interest rates within an area that shares the same inflation (that is, the same country) should be the same. Second, that the lenders know the inflation for the period of time that they are going to lend the money.
One reason behind the difference between the interest that yields a treasury bond and the interest that yields a mortgage loan is the risk that the lender takes from lending money to an economic agent. In this particular case, a government is more likely to pay than a private citizen. Therefore, the interest rate charged to a private citizen is larger than the rate charged to the government.
To take into account the information asymmetry aforementioned, both the value of inflation and the real price of money are changed to their expected values resulting in the following equation:
it = r(t + 1) + π(t + 1) + σ
Here, it is the nominal interest at the time of the loan, r(t + 1) is the real interest expected over the period of the loan, π(t + 1) is the inflation expected over the period of the loan and σ is the representative value for the risk engaged in the operation.
Cumulative interest or return
The calculation for cumulative interest is (FV/PV)-1. It ignores the ‘per year’ convention and assumes compounding at every payment date. It is usually used to compare two long term opportunities.
Market interest rates
There are markets for investments (which include the money market, bond market, as well as retail financial institutions like banks) set interest rates. Each specific debt takes into account the following factors in determining its interest rate:
Opportunity cost
Opportunity cost encompasses any other use to which the money could be put, including lending to others, investing elsewhere, holding cash (for safety, for example), and simply spending the funds.
Inflation
Since the lender is deferring his consumption, he will at a bare minimum, want to recover enough to pay the increased cost of goods due to inflation. Because future inflation is unknown, there are three tactics.
- Charge X% interest ‘plus inflation’. Many governments issue ‘real-return’ or ‘inflation indexed’ bonds. The principal amount or the interest payments are continually increased by the rate of inflation. See the discussion at real interest rate.
- Decide on the ‘expected’ inflation rate. This still leaves both parties exposed to the risk of ‘unexpected’ inflation.
- Allow the interest rate to be periodically changed. While a ‘fixed interest rate’ remains the same throughout the life of the debt, ‘variable’ or ‘floating’ rates can be reset. There are derivative products that allow for hedging and swaps between the two.
Default
There is always the risk the borrower will become bankrupt, abscond or otherwise default on the loan. The risk premium attempts to measure the integrity of the borrower, the risk of his enterprise succeeding and the security of any collateral pledged. For example, loans to developing countries have higher risk premiums than those to the US government due to the difference in creditworthiness. An operating line of credit to a business will have a higher rate than a mortgage loan.
The creditworthiness of businesses is measured by bond rating services and individual’s credit scores by credit bureaus. The risks of an individual debt may have a large standard deviation of possibilities. The lender may want to cover his maximum risk, but lenders with portfolios of debt can lower the risk premium to cover just the most probable outcome.
Default Interest
Default interest is the interest that a borrower would pay if he/she will not fulfill the loan covenants. The default interest is usually much higher than the original interest since it is reflecting the aggravation in the financial risk of the borrower. The default interest compensates the lender for the added risk.
Banks tend to add default interest to the loan agreements in order to separate between different scenarios.
Deferred consumption
Charging interest equal only to inflation will leave the lender with the same purchasing power, but he would prefer his own consumption sooner rather than later. There will be an interest premium of the delay. He may not want to consume, but instead would invest in another product. The possible return he could realize in competing investments will determine what interest he charges.
Length of time
Shorter terms have less risk of default and inflation because the near future is easier to predict. Broadly speaking, if interest rates increase, then investment decreases due to the higher cost of borrowing (all else being equal).
Interest rates are generally determined by the market, but government intervention – usually by a central bank- may strongly influence short-term interest rates, and is used as the main tool of monetary policy. The central bank offers to buy or sell money at the desired rate and, due to their control of certain tools (such as, in many countries, the ability to print money) they are able to influence overall market interest rates.
Investment can change rapidly in response to changes in interest rates, affecting national income, and, through Okun’s Law, changes in output affect unemployment
Open market operations in the United States
The Federal Reserve (Fed) implements monetary policy largely by targeting the federal funds rate. This is the rate that banks charge each other for overnight loans of federal funds. Federal funds are the reserves held by banks at the Fed.
Open market operations are one tool within monetary policy implemented by the Federal Reserve to steer short-term interest rates. Using the power to buy and sell treasury securities, the Open Market Desk at the Federal Reserve Bank of New York can supply the market with dollars by purchasing T-notes, hence increasing the nation’s money supply. By increasing the money supply or Aggregate Supply of Funding (ASF), interest rates will fall due to the excess of dollars banks will end up with in their reserves. Excess reserves may be lent in the Fed funds market to other banks, thus driving down rates.
Interest rates and credit risk
It is increasingly recognized that the business cycle, interest rates and credit risk are tightly interrelated. The Jarrow-Turnbull model was the first model of credit risk that explicitly had random interest rates at its core. Lando (2004), Darrell Duffie and Singleton (2003), and van Deventer and Imai (2003) discuss interest rates when the issuer of the interest-bearing instrument can default.
Money and inflation
Loans, bonds, and shares have some of the characteristics of money and are included in the broad money supply.
By setting i*n, the government institution can affect the markets to alter the total of loans, bonds and shares issued. Generally speaking, a higher real interest rate reduces the broad money supply.
Through the quantity theory of money, increases in the money supply lead to inflation. This means that interest rates can affect inflation in the future.
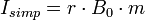

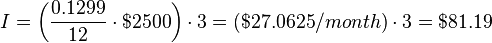
![begin{align}
&I_{comp}=B_0cdotbig[left(1+rright)^m-1big]\
&B_m=B_0+I_{comp}
end{align}](http://upload.wikimedia.org/math/5/8/e/58e52361340f8f8a60b41edb135d951f.png)
![begin{align}
&mbox{Calculation for Compound Interest}:\
I_{comp}&=$2500cdotbigg[bigg(1+frac{0.1299}{12}bigg)^3-1bigg]\
&=$2500cdotleft(1.010825^3-1right)\
&=$82.07\
end{align}](http://upload.wikimedia.org/math/2/e/2/2e29e6081dd8697e4d5cdf34f5586e26.png)