In finance, the yield curve is the relation between the interest rate (or cost of borrowing) and the time to maturity of the debt for a given borrower in a given currency. For example, the U.S. dollar interest rates paid on U.S. Treasury securities for various maturities are closely watched by many traders, and are commonly plotted on a graph such as the one on the right which is informally called "the yield curve." More formal mathematical descriptions of this relation are often called the term structure of interest rates.
The yield of a debt instrument is the overall rate of return available on the investment. For instance, a bank account that pays an interest rate of 4% per year has a 4% yield, when the price of the bond equals its par value. In general the percentage per year that can be earned is dependent on the length of time that the money is invested. For example, a bank may offer a "savings rate" higher than the normal checking account rate if the customer is prepared to leave money untouched for five years. Investing for a period of time t gives a yield Y(t).
This function Y is called the yield curve, and it is often, but not always, an increasing function of t. Yield curves are used by fixed income analysts, who analyze bonds and related securities, to understand conditions in financial markets and to seek trading opportunities. Economists use the curves to understand economic conditions.
The yield curve function Y is actually only known with certainty for a few specific maturity dates, while the other maturities are calculated by interpolation
The typical shape of the yield curve
Yield curves are usually upward sloping asymptotically: the longer the maturity, the higher the yield, with diminishing marginal increases (that is, as one moves to the right, the curve flattens out). There are two common explanations for upward sloping yield curves. First, it may be that the market is anticipating a rise in the risk-free rate. If investors hold off investing now, they may receive a better rate in the future. Therefore, under the arbitrage pricing theory, investors who are willing to lock their money in now need to be compensated for the anticipated rise in rates—thus the higher interest rate on long-term investments.
Another explanation is that longer maturities entail greater risks for the investor (i.e. the lender). A risk premium is needed by the market, since at longer durations there is more uncertainty and a greater chance of catastrophic events that impact the investment. This explanation depends on the notion that the economy faces more uncertainties in the distant future than in the near term. This effect is referred to as the liquidity spread. If the market expects more volatility in the future, even if interest rates are anticipated to decline, the increase in the risk premium can influence the spread and cause an increasing yield.
The opposite position (short-term interest rates higher than long-term) can also occur. For instance, in November 2004, the yield curve for UK Government bonds was partially inverted. The yield for the 10 year bond stood at 4.68%, but was only 4.45% for the 30 year bond. The market’s anticipation of falling interest rates causes such incidents. Negative liquidity premiums can also exist if long-term investors dominate the market, but the prevailing view is that a positive liquidity premium dominates, so only the anticipation of falling interest rates will cause an inverted yield curve. Strongly inverted yield curves have historically preceded economic depressions.
The shape of the yield curve is influenced by supply and demand: for instance, if there is a large demand for long bonds, for instance from pension funds to match their fixed liabilities to pensioners, and not enough bonds in existence to meet this demand, then the yields on long bonds can be expected to be low, irrespective of market participants’ views about future events.
The yield curve may also be flat or hump-shaped, due to anticipated interest rates being steady, or short-term volatility outweighing long-term volatility.
Yield curves continually move all the time that the markets are open, reflecting the market’s reaction to news. A further "stylized fact" is that yield curves tend to move in parallel (i.e., the yield curve shifts up and down as interest rate levels rise and fall).
Types of yield curve
There is no single yield curve describing the cost of money for everybody. The most important factor in determining a yield curve is the currency in which the securities are denominated. The economic position of the countries and companies using each currency is a primary factor in determining the yield curve. Different institutions borrow money at different rates, depending on their creditworthiness. The yield curves corresponding to the bonds issued by governments in their own currency are called the government bond yield curve (government curve). Banks with high credit ratings (Aa/AA or above) borrow money from each other at the LIBOR rates. These yield curves are typically a little higher than government curves. They are the most important and widely used in the financial markets, and are known variously as the LIBOR curve or the swap curve. The construction of the swap curve is described below.
Besides the government curve and the LIBOR curve, there are corporate (company) curves. These are constructed from the yields of bonds issued by corporations. Since corporations have less creditworthiness than most governments and most large banks, these yields are typically higher. Corporate yield curves are often quoted in terms of a "credit spread" over the relevant swap curve. For instance the five-year yield curve point for Vodafone might be quoted as LIBOR +0.25%, where 0.25% (often written as 25 basis points or 25bps) is the credit spread.
Normal yield curve
From the post-Great Depression era to the present, the yield curve has usually been "normal" meaning that yields rise as maturity lengthens (i.e., the slope of the yield curve is positive). This positive slope reflects investor expectations for the economy to grow in the future and, importantly, for this growth to be associated with a greater expectation that inflation will rise in the future rather than fall. This expectation of higher inflation leads to expectations that the central bank will tighten monetary policy by raising short term interest rates in the future to slow economic growth and dampen inflationary pressure. It also creates a need for a risk premium associated with the uncertainty about the future rate of inflation and the risk this poses to the future value of cash flows. Investors price these risks into the yield curve by demanding higher yields for maturities further into the future. However, a positively sloped yield curve has not always been the norm. Through much of the 19th century and early 20th century the US economy experienced trend growth with persistent deflation, not inflation. During this period the yield curve was typically inverted, reflecting the fact that deflation made current cash flows less valuable than future cash flows. During this period of persistent deflation, a ‘normal’ yield curve was negatively sloped.
Steep yield curve
Historically, the 20-year Treasury bond yield has averaged approximately two percentage points above that of three-month Treasury bills. In situations when this gap increases (e.g. 20-year Treasury yield rises higher than the three-month Treasury yield), the economy is expected to improve quickly in the future. This type of curve can be seen at the beginning of an economic expansion (or after the end of a recession). Here, economic stagnation will have depressed short-term interest rates; however, rates begin to rise once the demand for capital is re-established by growing economic activity.
In January 2010, the gap between yields on two-year Treasury notes and 10-year notes widened to 2.92 percentage points, its highest ever.
Flat or humped yield curve
A flat yield curve is observed when all maturities have similar yields, whereas a humped curve results when short-term and long-term yields are equal and medium-term yields are higher than those of the short-term and long-term. A flat curve sends signals of uncertainty in the economy. This mixed signal can revert to a normal curve or could later result into an inverted curve. It cannot be explained by the Segmented Market theory discussed below.
Inverted yield curve
An inverted yield curve occurs when long-term yields fall below short-term yields. Under unusual circumstances, long-term investors will settle for lower yields now if they think the economy will slow or even decline in the future. Campbell R. Harvey’s 1986 dissertation[1] showed that an inverted yield curve accurately forecasts U.S. recessions. An inverted curve has indicated a worsening economic situation in the future 6 out of 7 times since 1970.[2] The New York Federal Reserve regards it as a valuable forecasting tool in predicting recessions two to six quarters ahead. In addition to potentially signaling an economic decline, inverted yield curves also imply that the market believes inflation will remain low. This is because, even if there is a recession, a low bond yield will still be offset by low inflation. However, technical factors, such as a flight to quality or global economic or currency situations, may cause an increase in demand for bonds on the long end of the yield curve, causing long-term rates to fall.
Theory
There are three main economic theories attempting to explain how yields vary with maturity. Two of the theories are extreme positions, while the third attempts to find a middle ground between the former two.
Market expectations (pure expectations) hypothesis

This hypothesis assumes that the various maturities are perfect substitutes and suggests that the shape of the yield curve depends on market participants’ expectations of future interest rates. These expected rates, along with an assumption that arbitrage opportunities will be minimal, is enough information to construct a complete yield curve. For example, if investors have an expectation of what 1-year interest rates will be next year, the 2-year interest rate can be calculated as the compounding of this year’s interest rate by next year’s interest rate. More generally, rates on a long-term instrument are equal to the geometric mean of the yield on a series of short-term instruments. This theory perfectly explains the observation that yields usually move together. However, it fails to explain the persistence in the shape of the yield curve.
Shortcomings of expectations theory: Neglects the risks inherent in investing in bonds (because forward rates are not perfect predictors of future rates). 1) Interest rate risk 2) Reinvestment rate risk
Liquidity premium theory
The Liquidity Premium Theory is an offshoot of the Pure Expectations Theory. The Liquidity Premium Theory asserts that long-term interest rates not only reflect investors’ assumptions about future interest rates but also include a premium for holding long-term bonds (investors prefer short term bonds to long term bonds), called the term premium or the liquidity premium. This premium compensates investors for the added risk of having their money tied up for a longer period, including the greater price uncertainty. Because of the term premium, long-term bond yields tend to be higher than short-term yields, and the yield curve slopes upward. Long term yields are also higher not just because of the liquidity premium, but also because of the risk premium added by the risk of default from holding a security over the long term. The market expectations hypothesis is combined with the liquidity premium theory:
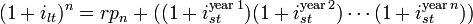
Where rpn is the risk premium associated with an n year bond.
Market segmentation theory
This theory is also called the segmented market hypothesis. In this theory, financial instruments of different terms are not substitutable. As a result, the supply and demand in the markets for short-term and long-term instruments is determined largely independently. Prospective investors decide in advance whether they need short-term or long-term instruments. If investors prefer their portfolio to be liquid, they will prefer short-term instruments to long-term instruments. Therefore, the market for short-term instruments will receive a higher demand. Higher demand for the instrument implies higher prices and lower yield. This explains the stylized fact that short-term yields are usually lower than long-term yields. This theory explains the predominance of the normal yield curve shape. However, because the supply and demand of the two markets are independent, this theory fails to explain the observed fact that yields tend to move together (i.e., upward and downward shifts in the curve).
Preferred habitat theory
The Preferred Habitat Theory is another guise of the Market Segmentation theory, and states that in addition to interest rate expectations, investors have distinct investment horizons and require a meaningful premium to buy bonds with maturities outside their "preferred" maturity, or habitat. Proponents of this theory believe that short-term investors are more prevalent in the fixed-income market, and therefore longer-term rates tend to be higher than short-term rates, for the most part, but short-term rates can be higher than long-term rates occasionally. This theory is consistent with both the persistence of the normal yield curve shape and the tendency of the yield curve to shift up and down while retaining its shape.